werry-chanの日記．料理とエンジニアリング

料理！コーディング！研究！日常！飯！うんち！睡眠！人間の全て！

ますらば東大模試(1)解いてみた

入試問題三角関数数学高校数学東京大学模試

最近暖かくて何着れば良いか分からないウェリーちゃんです．
さっき大学で野生のキジが歩いてて車で轢きそうになりました．

それでは本日は「ますらば東大模試」の問1を解いていきます．
twitter.com
こちらのtwiiterアカウント，数学を愛する会さんがあげてくれてて，暇じゃないけど息抜きで昨日解いてました．

問題全体はこちらです．
http://mathlava.neta.biz/moshi/2019toudai.pdf

werry-chan.hatenablog.com
僕の解いた問2はこちらです．

それでは解いていきましょう．

問1

$0\leq \theta < 2\pi$ において， $\theta$ が

$(1+sin\theta)(1+cos\theta)>1$ を満たすよう動く時，

$sin\theta cos\theta$ がとり得る値の範囲を示せ．

考えてくださいね．下の方に解答載せるので，気をつけてください．

******************

それでは解答を載せます．

sinとcosと見れば一番はじめに思い浮かぶのは，

円

ですね．

$y=sin\theta , x=cos\theta$

として変数変換すると，(x,y)は半径1の円上である．
また，不等式は

$(1+sin\theta)(1+cos\theta)>1$

$(1+y)(1+x)>1$

と変換される．これは $y>\frac{1}{y}$ をx方向-1，y方向-1と平行移動したものである．

この上で図形的に見ると，xyは半径1の円上→原点を対角線とする長方形の面積とわかる．(第2,4象限の面積は負(写真の青色の部分)．)
f:id:werry-chan:20190221142935j:plain

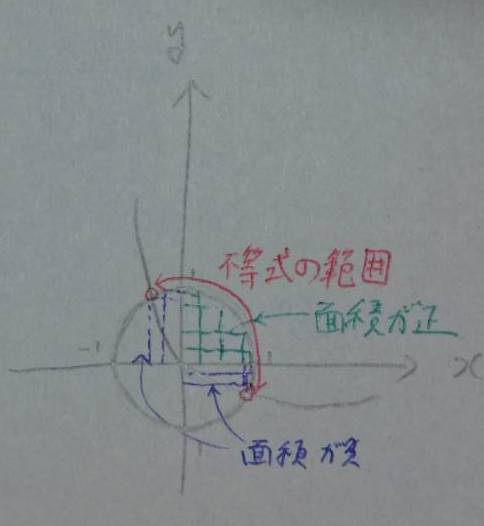
このような図形的背景を考えた上で， $\theta$ の範囲を考えると，

$(1+sin\theta)(1+cos\theta)=1$

の交点を求めることができれば，自ずと $\theta$ の範囲は求まる．
図形の見た目から，有名角じゃなさそうだなぁと予想が付きます．
実際， $\theta=\frac{\pi}{4},\frac{\pi}{3}$ が成立しないことは軽く確かめられます．

それでは交点を求める．

$(1+sin\theta)(1+cos\theta)=1$

$sin\theta +cos\theta +sin\theta cos\theta =0$

図形の見た目から，小さい角度範囲で調べたいなぁと思うように考えますね．
なので， $t=2\theta$ とおけば，倍精度で角度をピックアップするようになります．

$\sqrt{\frac{1+cos(t)}{2}}+\sqrt{\frac{1-cos(t)}{2}}=-\frac{sin(t)}{\sqrt{2}}$

$1+cos(t)+1-cos(t)+2\sqrt{1-cos^2(t)}=\frac{sin^2{t}}{2}$

$4(1+sin(t))=sin^2(t)$

$sin^2(t)-4sin(t)-4=0$

$sin(t)=2-2\sqrt{2}$

$cos(t)=\sqrt{8\sqrt{2}-11}$

これで目的の交点を片方見つけられました．
もう一方については，図形的に $y=x$ で線対称なので省略する．

ここまで導出できれば目的の値の範囲は容易に導けるでしょう．

一応，目的の面積について

$f(\theta)=sin\theta cos\theta=\frac{1}{2}sin2\theta$

なので， $\theta=\frac{\pi}{4}$ で最大値 $f(\frac{\pi}{4})=\frac{1}{2}$ を取る．

また， $f(\theta)$ を微分して増減を見れば

$\frac{\pi}{4}<\theta<\frac{3\pi}{4}$

において $f(\theta )$ が減少していることがわかる．

故に，上記で示した交点において $f(\theta)$ は最小値をとり，
$f(\theta_{mini})=(2-2\sqrt{2})\sqrt{8\sqrt{2}-11}$
が最小値である．

以上より，求める値の範囲は

$(2-2 \sqrt{2} )\sqrt{8 \sqrt{2}-11} < sin \theta cos \theta < \frac{1}{2}$

である．

[証明終了]

合ってるのかどうかわ分からないです．
もしも別解や
間違ってるでお前〜
みたいなことありましたら教えてください．