今回は,画像のフーリエ変換を応用して,走査トンネル顕微鏡(STM)でグラファイト(HOPG)を撮像し,FFTで鮮明化します.
具体的にはこのような作業をします.


左側の画像に赤線がありますが,すいません,元画像は紛失しました.
作業途中のスクリーンショットのみ見つかったので,これで勘弁してください.
走査トンネル顕微鏡(STM)とは?グラファイト(HOPG)とは?と思っている方へ.
STMは,簡単に言うと針で物の表面形状を見る顕微鏡です.
測定対象の近くに針を極限まで近づけると,測定対象物の表面原子の持つ電子がSTMの針に移動します(トンネル効果).
STMの針は電子を受け取って,その電流によって測定対象物の表面形状を測定できます.
ちなみにSTMの受け取る電流は,原子1個分の距離でも変化が読み取れるので,ナノスケールの測定に使われています.
HOPGは,簡単に言うと炭素です.
簡単に言うと,炭素の中でも,並び方がすごく綺麗な炭素のことをHOPGと呼びます.
詳しくは以下で↓
走査型トンネル顕微鏡 - Wikipedia
高配向性熱分解グラファイト - Wikipedia
さて,これまでにやってきたことを振り返る人へのリンクを置いておきます.
画像のフーリエ変換1は,FFTで具体的な画像へローパス・ハイパスフィルタをかけてみました.
画像のフーリエ変換 - werry-chanの日記.料理とエンジニアリング
画像のフーリエ変換2は,単調な波を使ってFFTの特性を理解しました.
pythonで画像のフーリエ変換2 - werry-chanの日記.料理とエンジニアリング
それでは,HOPGのSTM画像をFFTして鮮明にしましょう.
今回は,Igorというソフトウェアで解析を行います.
まずはHOPGのSTM画像をFFTしましょう.
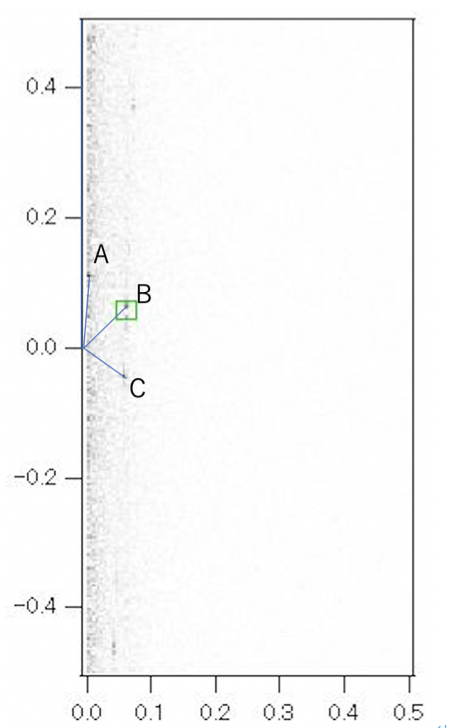
このFFT画像は,以前に行ったFFT画像と異なる様子がいくつかありますね.
1.縦に長い.
2.A,B,Cとか四角とか青い線が書いてある.
3.スケールバーがついている.
まず1.について説明します.
以前までのFFT画像を思い返してください.
全てのFFT画像は,原点対称だったような気がしませんか?
実は,以前までのFFT画像は原点対称でした.
ということは,重複する情報は除いた方が合理的です.
このような理由から,Igorでは左半分が省かれた,縦長のFFT画像になっています.
次に2.についてです.
A,B,Cとか資格とか青い線は,僕がこの後の作業の説明のために付しました.
3.はIgorのFFT画像の仕様です.
さて,続きに入りましょう.
パワースペクトル画像に対して,A,B,Cと点を付しています.
このABCは,FFT画像の主成分・ピーク(値が大きい領域)になります.
青い線は,中心からの方向が分かるように付してあります.
これらのA,B,Cそれぞれの近傍成分のみを抽出し,逆フーリエ変換してみましょう.


このように主成分によっていくつかの波が抽出されます.
これらのA,B,C3つ全ての近傍を抽出して逆フーリエ変換するとこのようになります.
何か粒子っぽい像が見えますね.
粒子っぽいですが,粒子ではないです.
あくまでSTMは対象物の電子を測定しているので,見えている像は電子です.
電子に注目して今回のHOPG像を考察しましょう.
グラファイトは上のように二つの構造が有名な物ですが,今回はα構造だと考えます.
理由は,FFT像であげられる主成分ABCの相対角度が約60°であったという解析結果です.
βは複雑で,α構造のような単調な画像スペクトルは得られないと考えます.
さて,次に測定結果から原子間距離を推定しましょう.
今回取得した元画像は,縦:横 = 4nm : 4nmでした.
そして,FFT像の原点とABC間の距離は約0.12です(今回は象限入れ替えしてないので,原点周辺が高周波成分で辺縁部が低周波成分です).
周波数に直すと主成分周波数は1/0.12 ~ 8.3です.
4nmの画像に対して,主成分の波はピーク(絶対値ピーク)が16.6個存在します.
逆フーリエ変換後の画像を見て,実際に横一列で16or17個くらいの白点が確認できると思います.
それでは白点間の距離を算出します.
4 nm/16.6 ~= 0.24 nm ~= 2.4 Å
この白点間の距離は,STMで測定されたトンネル電流(電子)の主成分であることに注意してください.
先ほどのα型のグラファイトの構造を見てみます.
青線で描かれたグラファイトは最上層で,赤線で描かれたグラファイト層はその下の層です.
赤と青の二つの層で原子の重なり合う位置に注目して,それぞれを最短距離で結ぶと正三角形が浮かび上がります.
STMで測定された像の主成分とは,この正三角形の頂点に由来する物なのです.
STMは,グラファイトの電子雲が上層と下層で重なり合う位置が,トンネル電流が大きく,その位置を主成分として検出しているということです.
さて,それではベンゼン状に結合したグラファイトの原子間距離1.42 Åは既知としましょう.
そうすると,検出された正三角形の一辺の長さは,理論上はとなります.
解析結果の2.4 Åとほぼ一致していますね.
このようにして,画像のフーリエ変換はSTMの解析などに応用されています.
様々な分野で応用されていますので,また時間があれば紹介しましょう.