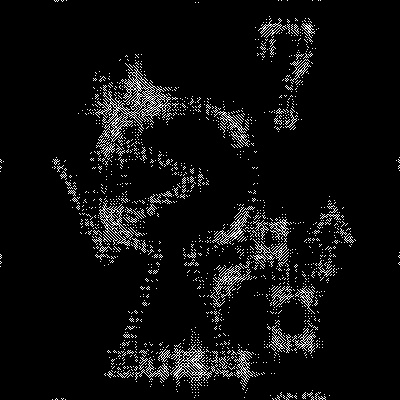2019-01-01

Heisenbergの不確定性関係の問題が解けない

量子力学1 物理質問

最近勉強不足が甚だしいので，Heisenbergの不確定性関係についての教科書問題解いてたら年を越してしまったウェリーちゃんです．
実家に帰るとご飯を作らなくても出てくるのでビックリしてます．
あと昼まで寝てて夜寝れないんじゃ〜〜．

本題に入りましょう．
今日解いてた量子力学の問題で分かんないところあったので，質問がてら投稿しちゃいます．

[問]
Heisenbergの不確定性関係の式
$\sqrt{(\bar{\Delta q})^2・(\bar{\Delta p})^2}\geq \frac{\hbar}{2}$
が最小値 $\frac{\hbar}{2}$ をとる時，Gauss関数を用いて
$\psi (q)=Aexp\left[ \frac{-q^2}{2(\bar{\Delta q})^2}\right]$
を示せ．ただしAは定数で $\bar{q}=\bar{p}=0$ である．
(注：演算子 $\hat{A}$ の期待値を $\bar{A}$ ，期待値からの偏差を $\Delta A=\hat{A}-\bar{A}$ としてる．)
出典：砂川重信先生の岩波書籍より"量子力学"pp.53です．

この結果をいくら計算しても答えが
$\psi (q)=Aexp\left[ \frac{-q^2}{4\bar{(\Delta q)^2}}\right]$
にしかならないのです．

導出法は以下のようにしてます．
$\left[ \hat{q},\hat{p}\right]=\left[ \Delta\hat{q},\Delta\hat{p}\right] =i\hbar$
実数 $\alpha$ を用いて
$I(a)=\langle\psi | (\alpha\Delta\hat{q}-i\Delta\hat{p})・(\alpha\Delta\hat{q}+i\Delta{\hat{p}}))|\psi\rangle\\=\langle\psi |(\alpha^2(\Delta\hat{q})^2+i\alpha\left[ \Delta\hat{q},\Delta\hat{p}\right] +(\Delta\hat{p})^2)|\psi\rangle=0$
がHeisenbergの不確定性関係関係から導け，
$\alpha^2(\Delta\hat{q})^2+i\alpha\left[ \Delta\hat{q},\Delta\hat{p}\right] +(\Delta\hat{p})^2=0$
より $\alpha=\frac{\hbar}{2\bar{(\Delta q)^2}}, \,\,\,\, (\alpha\Delta q+i\Delta p)|\psi\rangle=0$
上記の右の式は $\bar{q}=\bar{p}=0$ より
$(\alpha\hat{q}+i\hat{p})|\psi\rangle=0$
$\langle q |(\alpha\hat{q}+i\hat{p})|\psi\rangle=(\alpha q+ip)\psi (q)=0$
この式に $\alpha=\frac{\hbar}{2\bar{(\Delta q)^2}}$ を代入して計算すると
$\psi (q)=Aexp\left[ \frac{-q^2}{4\bar{(\Delta q)^2}}\right]$
となる．

何が間違ってるかわからないのです．
考えてみてくれた人はコメントでも何でも「合ってると思う」とか「これは〜〜だから違う」みたいなリプライくださいな．

2018-12-30

pythonで逆光写真のアート化

情報画像処理アート python pillow PIL

普段住んでる部屋がボロすぎて，実家帰ると部屋が暖かくて身震いしてしまうウェリーちゃんです．
今住んでる部屋は，築60年over，冷気ガンガン入ってくる，風呂桶が突然壊れて風呂入れなくなる，シャワーは5秒ごとに冷水が出る，etc.と大変です．

関係ない話はこれくらいにして，
それでは今回の記事の内容に入りましょう．

今回はpython使って逆光写真をアーティスティックにします．
f:id:werry-chan:20181230212525j:plain
↑SokuUPさんのサイトから持ってきた画像です．
SokuUp :: 風景自然空夕焼け逆光原爆ドーム :: permalink

この画像の影の部分を，クレースケールの画素の輝度によって閾値で2分割します．
輝度は0で黒，255で白です．
次にマスク画像の作成です．

f:id:werry-chan:20181230215006j:plain
↑今回は閾値は輝度0〜100を全て黒(255)，それ以上は全て白(0)の画像をマスク画像として作成します．黒っぽいところを白に，白っぽいところを黒にするって感じですね．

次に元の逆光写真の影の部分，マスク画像で言うと白くなった部分に合成する画像を用意します．
f:id:werry-chan:20181230215552j:plain
http://freeillustbook.net/starry-sky01/
↑このサイトから持ってきた画像と

f:id:werry-chan:20181230220141j:plain
http://shinkaiyablog.com/post-33/
↑このサイトから持ってきた画像を合成に使いましょう．

さて，それでは．．．
「フュージョン！！ハッ！！」
f:id:werry-chan:20181230220615j:plain

はい出来ました．
f:id:werry-chan:20181230220824p:plain
〇〇ンクスです．
カッケェーーー！！！！
あのさっきまでの逆光の風景写真がここまでカッコ良くなりました！！
Pythonやってて良かった〜ーー！！
みんなも頑張ってフュージョンしてみてくださいね．
下手だとデブのカッコ悪い奴になりますから気をつけて．

ごめんなさい．ドラゴンボール大好きなのでふざけてしまいました．
とまぁ茶番はこの辺にして，本当に合成してみましょう．
f:id:werry-chan:20181230221319j:plain
f:id:werry-chan:20181230221334j:plain
綺麗な雰囲気の画像が出来ましたねぇ．
逆光写真の影の部分を合成することでアーティスティックに仕上げることが出来ます．

ソースコードは以下のようになります．

from PIL import Image
import numpy as np

#入力画像(逆光画像)の読み込み
img=Image.open('gyakkou02.jpg','r')

#合成する画像の読み込み
img_back=Image.open('deep_sea03.jpg','r')

#imgのコピー作成
img_origin=img.copy()

#imgの画像サイズ取得
width,height=img.size

#img_backの画像サイズをimgと同じにリサイズ
img_back=img_back.resize((width,height))

#imgをグレースケールに変換してimg_grayとする
img_gray=img.convert("L")

#輝度0〜100を255，それ以外を0にする．(二値化する)
img_gray=img_gray.point(lambda x: 0 if x > 100 else 255)

#img_grayを保存
#img_gray.save('gakkyou_gray02.jpg', 'JPEG', quality=100, optimize=True)

#新しい変数maskにimg_grayを代入．（名前をmaskにしたかっただけです．）
mask=img_gray

#合成して，合成画像をimg_resultとする．
img_result = Image.composite(img_back, img_origin, mask)

#img_resultを保存．
img_result.save('gakkyou_fusion3.jpg', 'JPEG', quality=100, optimize=True)

入力画像，二値化の閾値，二値化の値変更((0,255)→(100,255)など，透過率の変更ということ)，二値化ではなく3,4,5値化で透過率をグラデーションする
などなどすることで，さらに面白いことが出来ます．

以下に他の画像での例をあげますね．
f:id:werry-chan:20181230223752j:plain
↑これが元画像です．
↓以下が合成画像です．
f:id:werry-chan:20181230222950j:plain
f:id:werry-chan:20181230223059j:plain
f:id:werry-chan:20181230223344j:plain
なんかいろんなバリエーションで出来ますねぇ．

参考にしたサイトは以下になります．
Python, Pillowで画像を一括リサイズ（拡大・縮小） | note.nkmk.me
Python, Pillowで二枚の画像をマスク画像に従って合成 | note.nkmk.me
PIL/Pillow チートシート - Qiita
Python 3.5 対応画像処理ライブラリ Pillow (PIL) の使い方 - Librabuch

2018-12-30

ハチノスのトマト煮込み

年末で家に帰ってニャンコをモフモフしながら記事書いてるウェリーちゃんです．
あと新幹線の中で統計力学の本読んでたら寝落ちして首痛めました．
統計力学のグランドカノニカルアンサンブル理論(grand canonical ensemble theory)って名前，中二病心くすぐられてカッコいいですよね．

そんなこんなで実家に帰ってきたら
オカン「おい．お前ハチノス料理できるやろ．買ったからトマト煮にしろ．」
ワイ「そんな藪からアナコンダみたいな．わかった．やったるわ．」

ってんで，今日の記事はハチノス料理です．
f:id:werry-chan:20181230142205j:plain
↑ハチノスのトマト煮込みです．
(なんかバックに美味しそうな角煮がありますが，角煮はまた今度です．)

それではレシピです．
まずは下茹でします．

ハチノスを適当に切って，沸騰した鍋に数分入れ，出して水で洗う．
新しい水で沸騰させ，1を数回繰り返します． (臭みが取れるまで)
ハチノス1kgに対して酢大さじ6，生姜一片．ハチノスがヒタヒタになるよう水を鍋に張り，先ほどの酢と生姜を入れます．塩は海水くらいにしょっぱめの濃度にします．
火にかけて，大体アクが出たらとってやります．僕は圧力鍋使うので，高圧で大体15分程度で出来ます．

これで下茹では完了です．臭みがとれたので，そのままマリネにも出来ますが，今回はトマト煮です．

みじん切りしたニンニクをオリーブオイルで炒めます．
ニンニクが黄金色に変わる前くらいにタマネギ，セロリを入れて透き通る程度に炒める．
下茹での済んだハチノスとトマト缶と白ワインを2に加えて煮込みます．
最後盛り付けでパセリとかチーズ振ったら綺麗ですね．

2018-12-29

画像のフーリエ変換

親戚の家でモフモフの猫に囲まれながらブログ書いてるウェリーちゃんです．

早く暖かいペット可アパートに引っ越して，毎日モフモフ生活したいです．

閑話休題

それでは，今回の題材は"画像のフーリエ変換"です．

フーリエ変換って何ぞ？って人に教えてあげます．

$F(\xi)=\int^\infty_{-\infty}f(x)e^{-2\pi ix\xi}dx$

式で表すとこういうことです．

すいません．フーリエ変換については，また今度説明します．

でも一応，非常に簡単にですが説明します．

元の関数 $f(x)$ を周波数成分ごとに分解し，周波数 $\xi$ の成分が $F(\xi)$ になっているということを表しています．

詳しくは以下のリンクなどを参考にしてください．

フーリエ変換 - Wikipedia

【画像45枚あり】フーリエ変換を宇宙一わかりやすく解説してみる | ロボット・IT雑食日記

このページで画像のフーリエ変換について詳しく説明しています↓
werry-chan.hatenablog.com

応用編↓
画像のフーリエ変換3: 走査トンネル顕微鏡(STM)でグラファイト(HOPG)を撮像し，FFTで鮮明化する． - werry-chanの日記．料理とエンジニアリング

僕的には画像のフーリエ変換については

周波数領域における画像処理
↑このサイトが一番分かりやすいです．

まぁ今回の題材は"画像のフーリエ変換"なので，とりあえず一発フーリエ変換やってやりましょう．

あ，最後にpython3のソースコード載せます．

f:id:werry-chan:20181229133815j:plain
↑こいつは僕の自作キャラクター"目玉ハッカー君"です．

可愛いですね．ハッカー（ハッキングする奴）なので，悪魔っぽく角と尻尾つけて悪そうにしてやりました．めっちゃ可愛い．

話がそれましたね．

それでは，この"目玉ハッカー君"の画像を二次元フーリエ変換します．

f:id:werry-chan:20181229134358j:plain
↑フーリエ変換後の"目玉ハッカー君"画像

これがフーリエ変換画像になります．(正しくは，二次元フーリエ変換のパワースペクトル画像です．)

なんかよく分からんが幾何学的な模様ができましたね．

これは画像の中心から外縁にかけて，次第に周波数成分の高いスペクトルを表してます．

通常この二次元フーリエ変換画像を扱う際は，第一象限と第四象限，第二象限と第三象限を入れ替えて扱います．

f:id:werry-chan:20181229215446j:plain
↑入れ替えたものがこれです．

フーリエ変換画像とその象限入れ替えを模式図にしたものは，以下のようになります．

f:id:werry-chan:20181229215844p:plain
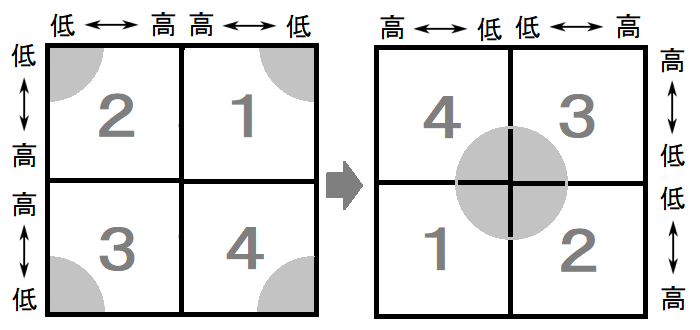
【画像処理】フーリエ変換の原理・実装例 | アルゴリズム雑記より引用画像です．

この図によると入れ替え後，真ん中に低周波成分が集まっているとなってますね．

入れ替え後のフーリエ変換画像の真ん中の低周波成分のみ抽出すると

f:id:werry-chan:20181229224608j:plain
フーリエ変換画像ではこのようになります．

それでは，この低周波数成分のみになったと思われるフーリエ変換画像を逆変換して再生してみましょう．

f:id:werry-chan:20181229224757j:plain
↑再生され，低周波数成分抽出された"目玉ハッカー君"画像

次は逆に高周波成分のみを抽出してみましょう．

f:id:werry-chan:20181229225347j:plain
↑高周波成分のみ抽出したフーリエ変換像

これを逆変換により再生して

f:id:werry-chan:20181229225449j:plain
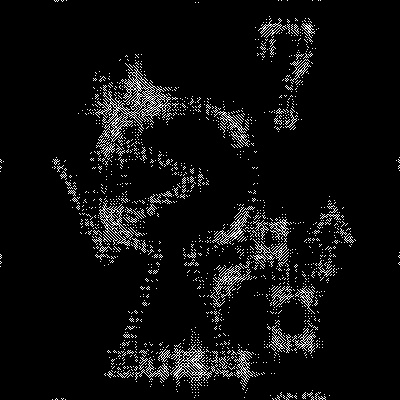
↑再生され，高周波成分のみ抽出された"目玉ハッカー君"画像

低周波成分と高周波成分って何を表してるの？と言う方のために，

これらの高周波成分抽出画像と低周波成分抽出画像を見比べて見よう．

"目玉ハッカー君"画像において，最も細かい描き込みの多い角の部分に注目してもらいたい．角の細かい模様を低周波成分では全く描けていないが，高周波成分では細かい描き込みがみられる．

また輪郭線のシャープさを比べると，低周波成分では輪郭線がボヤけて何重にも描かれているが，高周波成分ではかなり正確に元の輪郭線上をズレないでプロットしている．(画像の端に向かうと計算機上のフーリエ変換の癖で描画が甘くなる)

大方な見た目の点で言うと，低周波成分は全体的な雰囲気をボヤけた状態だが表せている．

などなどの点が比較によって見受けられる．

まぁ言いたいことを簡単にまとめると，”画像の高周波成分は細かい描き込みの成分”で”画像の低周波成分は大方の輪郭などの成分”と言うことだ．

応用面で言うと，フーリエ変換を使うことで細かい成分で構成されたノイズなどを排除できたり，輪郭線の抽出で画像処理に用いられてたりする．

ソースコード

import cv2
import numpy as np

#入力画像の読み込み
img=cv2.imread("werry-icon.jpg",0)#0はグレースケールで読み込み

#入力画像のサイズ取得
width,height=img.shape

#画像の二次元フーリエ変換
fimg=np.fft.fft2(img)

#パワースペクトル化する
#fimg= 20*np.log(np.abs(fimg))

#第1象限と第3象限，第2象限と第4象限の入れ替え
fimg = np.fft.fftshift(fimg)#高周波透過フィルタの場合，ここはコメントアウト

#入力画像と同じサイズの値0のnumpy array作成
dst=np.zeros(img.shape, dtype=complex)

#中心の値のみ透過(今回はローパス)
a=0.2#aは中心からのフィルターサイズ比率
dst[int(height*(0.5-a)):int(height*(0.5+a)), int(width*(0.5-a)):int(width*(0.5+a))] = fimg[int(height*(0.5-a)):int(height*(0.5+a)), int(width*(0.5-a)):int(width*(0.5+a))]

#再び第1象限と第3象限，第2象限と第4象限の入れ替え
dst= np.fft.fftshift(dst)#高周波透過フィルタの場合，ここはコメントアウト

#二次元逆フーリエ変換
dst = np.fft.ifft2(dst)

#実数部のみ抽出
low_img=np.uint8(dst.real)

#画像の書き込み
cv2.imwrite("werry-icon-low.jpg",low_img)

2018-12-29

平成最後の等比級数

数学高校数学等比級数多項式年の瀬

「平成最後の〜云々」って何か使いたかっただけのタイトルです．

平成最後の年は，平成31年，西暦でいえば西暦2019年です．

ということで突然ですが数学の問題を出題します．

[問]

以下の等比級数を

"平成最後の等比級数"と定義します．

$S_{2019}=1+31^1+31^2+...+31^{2019}$

この"平成最後の等比級数"が

$S_{3}=1+31^1+31^2+31^3$

で割り切れることを証明せよ．

これは”平成最後の宿題”って感じですね．

これはtwitterで回って来た問題でした．

まぁいうて3分くらいで解けます．

でも，この”平成最後の宿題”を解けないような数学扱う分野の人は年越し蕎麦食う権利ないので，見た人は解いてスッキリ年越ししてください．

以下に答えが載ってるので，まだ解いてない人は注意です．

そろそろ書き始めますよ？

[答え]

色んなレベルの人がいると思うので，あえて帰納的な解説にしましょう．

僕は脳筋なので，ゴリゴリに因数分解をしてみようと思いまして，実際やってみたら規則性がみえたって感じです．実際やってることとしては，高校数学でいう"多項式の割り算"って感じですかね？

$S_{3}=1+31^1+31^2+31^3\\S_{3}\times 31^{2016}=31^{2019}+31^{2018}+31^{2017}+31^{2016}\\S_{3}\times (31^{2016}+31^{2012})=31^{2019}+31^{2018}+31^{2017}+31^{2016}+31^{2015}+31^{2014}+31^{2013}+31^{2012}$

同様にして

$S_{3}\times (31^{2016}+31^{2012}+...+31^{2016-4n})=31^{2019}+31^{2018}+..+31^{2016-4n}$

となります．

2016は4で割り切れるので

$S_{3}\times (31^{2016}+31^{2012}+...+31^{2016-4n}+...+1)=S_{2019}$

となります．(一応，整数aの $a^0=1$ と補足します．)

この解説見て，気づいてると思いますが，等比級数の公比は31である意味はないですね．

解けてないにも関わらず，この解説見てる理工系の学生は年越さないでくださいねΣ੧(❛□❛✿)

以下に多項式の割り算について書いてあるページのリンクをあげておきます．

多項式の割り算の二通りの計算方法と例題 | 高校数学の美しい物語

http://www.ftext.org/text/section/108

多項式の除法（割り算）

2018-12-29

メカジキばら肉のステーキ&スープ

料理魚和食スープ

最近"ボボボーボ・ボーボボ"見ながら作業してるウェリーちゃんです．

ボーボボは内容が支離滅裂なので，見てても見てなくても見逃してもあんまり関係ないので作業用にちょうど良いです．

ボーボボってこんなん↓

ボボボーボ・ボーボボ - Wikipedia

なんか1話目が無料で読めるらしい↓

shonenjumpplus.com

閑話休題

それでは先日作って美味しかった"メカジキばら肉のステーキ&スープ"の紹介しましょう．

f:id:werry-chan:20181229041859p:plain — 生のメカジキばら肉

こいつが生のメカジキばら肉ですね．

あ，でも，よくよく見ると塩塗った後のような気がする．．．

まぁいいでしょう．

メカジキばら肉ステーキレシピ↓

このメカジキばら肉に塩を塗って，強火で短い時間(厚みによるが今回使った肉では3-4分程度)焼きます．
おすすめの焼き加減はミディアムレアです．ミディアムレアとは，中に少し火が通りきらない程度の焼き加減です．

強火でミディアムレアにすると，外は焼き目で良い食感，中はジューシーな肉汁と魚の脂身(トロ)で最高に美味しいです．

これはジューシーさを動画に撮った当時のツイートです．↓

カジキのバラトロ肉死ぬほどジューシーでクソ旨い pic.twitter.com/iSDqoagXdT
— 魔法少女キュア･クロオビ(うぇりー) (@0903Dear) November 15, 2018

このメカジキのステーキ，今回使ったものは骨の近くの部位で，大部分が骨になってます．そのため全部の肉を綺麗に食べきるのは難しいです．もったいない( T_T)

こういう時，ウェリーちゃんは食べるの面倒な肉は骨と一緒にそのまま残して，スープの出汁にします．

f:id:werry-chan:20181229043100p:plain

これがメカジキの出汁で取ったスープです．綺麗ですねぇ．

トロの脂身が油滴になり，良い感じに溶け出してキラキラと輝きます．

出汁の取り方↓

昆布とメカジキの骨を水(沸騰してない普通の水)に入れて火にかける．
沸騰直前に昆布を取り出す．
沸騰したら火を止めて，ミリンをお好みで少し入れる．
アクが出てたら取り，飲める程度に冷めてきたら完成です．

簡単なクセに，とんでもなく美味しいです．

ウェリーちゃんの料理史上，かつてない旨いスープです．

激推しスープなので是非とも作ってみてください．

なんとなくですが，今後こいつを進化させることができる素材として，ピーナッツorカシューナッツを考えてます．ピーナッツorカシューナッツの粉末を少し足すことで，より一層美味しいスープができるのでは？と期待してます．

2018-12-27

エーレンフェストの定理

量子力学1

こないだ買って1ヶ月も経ってない中古の土鍋が割れたウェリーちゃんです．

エーレンフェストの定理導出しましょう．

エーレンフェストの定理とかハイゼンベルグの云々ってかっこいいので，中二病心を揺さぶられるので，こいつらを導出してやりましょう(今回はエーレンフェストの定理)．

それではエーレンフェストの定理です．

$\frac{d\langle\bf{\hat{p}}\rangle}{dt}=\langle\bf{F}\rangle$

こいつを導出していきます．

まず文字の意味です．

$\bf{F}=-\nabla V$ でVはポテンシャルです． $\langle\bf{\hat{p}}\rangle$ は運動量演算子の期待値です．

それでは始めましょう．

$\frac{d\langle\bf{\hat{p}}\rangle}{dt}=\int\frac{d}{dt}(\psi^{\ast}\bf{\hat{p}}\psi)d\bf{r}\\=\int\frac{d\psi^{\ast}}{dt}\bf{\hat{p}}\psi d \bf{r}+\int\psi^{\ast}\bf{\hat{p}}\frac{d\psi}{dt} d \bf{r}$

ここでシュレディンガー方程式を時間tで微分した式を考えると，

$i\hbar\frac{d\psi}{dt}=\mathscr{H}\psi , \, -i\hbar\frac{d\psi^{\ast}}{dt}=\mathscr{H}\psi^{\ast}$

となり，この式を上式に代入すると，

$\frac{d\langle\bf{\hat{p}}\rangle}{dt}=\int (\frac{1}{-i\hbar}\mathscr{H}\psi^{\ast})\bf{\hat{p}}\psi d\bf{r}+\int \psi^{\ast}\bf{\hat{p}}\frac{\mathscr{H}}{i\hbar}\psi d\bf{r}\\=-\frac{1}{i\hbar}\int (\mathscr{H}\psi^{\ast}\bf{\hat{p}}\psi-\psi^{\ast}\bf{\hat{p}}\mathscr{H}\psi ) d\bf{r}\\=-\frac{1}{i\hbar}\int\psi^{\ast}[\mathscr{H},\bf{\hat{p}}]\psi d\bf{r}$

ここで $[\mathscr{H},\bf{\hat{p}}]$ を具体的に計算すると，

$[\mathscr{H},\bf{\hat{p}}]=\mathscr{H}\bf{\hat{p}}-\bf{\hat{p}}\mathscr{H}\\=(-\frac{\hbar^2}{2m}\Delta+V)(-i\hbar\nabla)+(i\hbar\nabla)(-\frac{\hbar^2}{2m}\Delta+V)\\=i\hbar\nabla V$

となる．

すなわち

$\frac{d\langle\bf{\hat{p}}\rangle}{dt}=-\frac{1}{i\hbar}\int\psi^{\ast}[\mathscr{H},\bf{\hat{p}}]\psi d\bf{r}\\=-\frac{1}{i\hbar}\int\psi^{\ast}(i\hbar\nabla V)\psi d\bf{r}\\=\int\psi^{\ast}(-\nabla V)\psi d\bf{r}\\=\int\psi^{\ast}\bf{F}\psi d\bf{r}\\=\langle\bf{F}\rangle$

となり，無事エーレンフェストの定理が導かれました．

上では冗長な計算をしてたんですが，ハイゼンベルグの運動方程式

werry-chan.hatenablog.com

を使うと式の一部は簡単になります．

$\frac{d\langle\bf{\hat{p}}\rangle}{dt}=\frac{i}{\hbar}[\mathscr{H},\langle\bf{\hat{p}}\rangle]\\=-\frac{1}{i\hbar}(\mathscr{H}\langle\bf{\hat{p}}\rangle-\langle\bf{\hat{p}}\rangle\mathscr{H})\\=-\frac{1}{i\hbar}\int (\mathscr{H}\psi^{\ast}\bf{\hat{p}}\psi-\psi^{\ast}\bf{\hat{p}}\mathscr{H}\psi ) d\bf{r}\\=-\frac{1}{i\hbar}\int\psi^{\ast}[\mathscr{H},\bf{\hat{p}}]\psi d\bf{r}$

参考文献は川村清先生の量子力学1↓

Amazon CAPTCHA

興味があればwikipediaへ↓

エーレンフェストの定理 - Wikipedia