解決方法："このPCは現在、Windows 11を実行するための最小システム要件を満たしていません"

"このPCは現在、Windows 11を実行するための最小システム要件を満たしていません"
上記のようなメッセージが表示されている際の対処方法をメモします。

こちらの作業はBIOS操作を伴うため, 作業対象PCから記事を見れない状態が発生します。
本記事をPCで開いている場合には, スマホなど別デバイスで開いてから作業を開始することをお勧めします。

画面左下のタスクバーに"PC"と入力して「PC正常性チェック」アプリを起動します。
「今すぐチェック」ボタンをクリックして, 以下のような画面が示された場合, 「TPM設定」の変更作業が必要になる場合が多いです。

PC正常性チェック -> 今すぐチェック -> Windows11要件を満たしていません

それではTPM設定が必要なのかどうかを確認しましょう。
設定 -> 更新とセキュリティ をクリックしてください。

設定(Windows Setting) -> 更新とセキュリティ

更新とセキュリティ -> Windowsセキュリティ -> デバイスセキュリティ をクリックします。

設定 -> 更新とセキュリティ -> Windows セキュリティ -> デバイス セキュリティ

以下の画面中に「セキュリティ プロセッサ」という項目がないことを確認してください。
「セキュリティ プロセッサ」項目が表示されている場合は, 「コア分離」項目の下に表示されています。

Windows セキュリティ画面に「セキュリティ プロセッサ」項目がないことを確認

======================
=== セキュリティ プロセッサ ある人向け 数行続きます ===
=== ない人は少し飛ばしてください ===

Windowsセキュリティ > セキュリティプロセッサが表示されている場合

もしもセキュリティプロセッサが表示されている場合には, 「セキュリティプロセッサの詳細」を確認しましょう。
仕様バージョン項目が2.0以下の場合には, Windows11 Updateが対応不能な場合があります。
そのような場合には, Microsoft Supportに相談してみるのが良いかもしれません。

Windows セキュリティ > セキュリティ プロセッサ > セキュリティ プロセッサの詳細

=== セキュリティプロセッサある人向け終了 ===
================

セキュリティプロセッサがないことを確認した人は, 次の作業に移ります。
次はTPM2.0を有効化する作業です。
以下の作業からはBIOS操作が必要になりますので, 注意してください。

画面左下のタスクバーから「設定」アプリを起動します。
設定 > 更新とセキュリティ へ移動します。

設定(Windows Setting) -> 更新とセキュリティ

設定 > 更新とセキュリティ > 回復 > 今すぐ再起動 の順にクリックしていきます。
再起動に際して, 作業中のファイルなどありましたら必ず保存しておいてください。

[設定] > [更新とセキュリティ] > [回復] > [今すぐ再起動]

オプションを選択 > トラブルシューティング をクリックします。

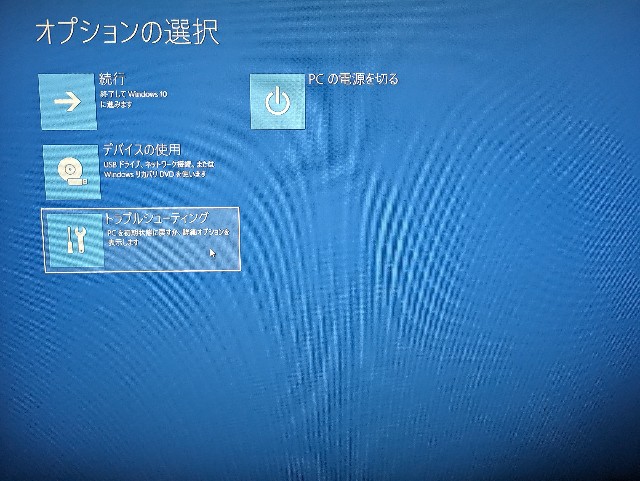
オプションを選択 > トラブルシューティング > 詳細オプション をクリックします。

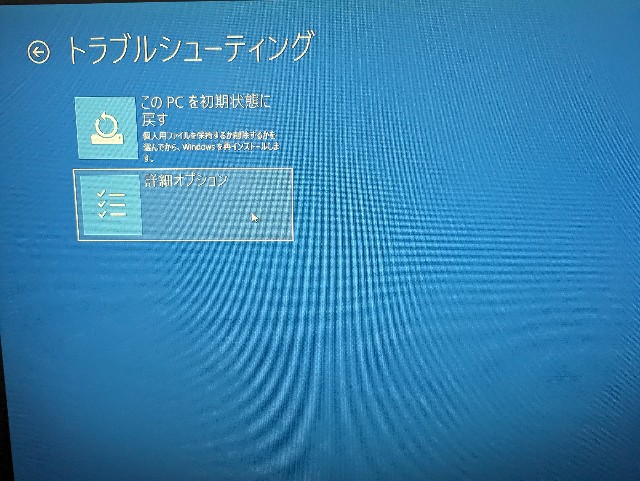
オプションを選択 > トラブルシューティング > 詳細オプション > UEFIファームウェアの設定 をクリックします。

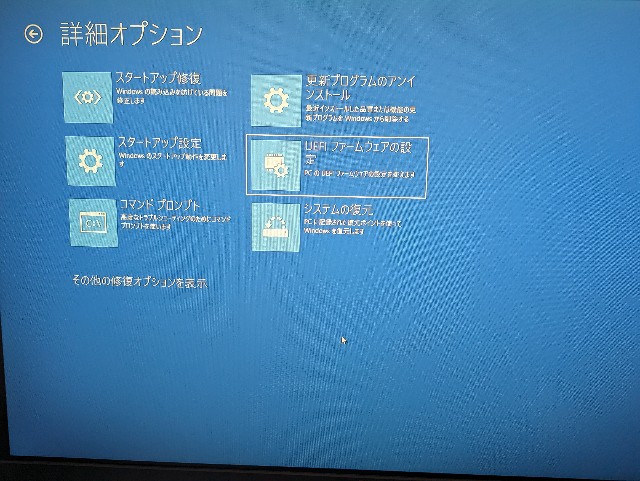
再起動し, BIOSが起動します。
注意
bios終了時は必ず変更保存[F10]してください。最悪OSレベルでぶっ壊れて悲惨なことになります。

以下からBIOS操作になります。
僕はMSI CLICK BIOSなのでポインタが使えるGUIになります。
右上の"Advanced"をクリックします。
以下より映り込み失礼します

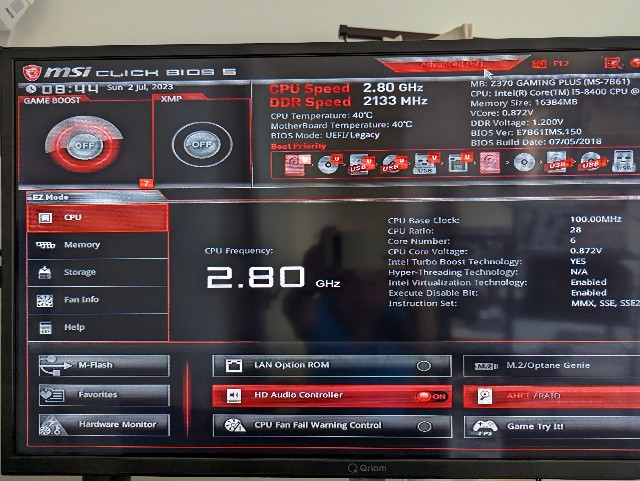
Advanced > Settings をクリックします。

Advanced > Settings > Security をクリックします。

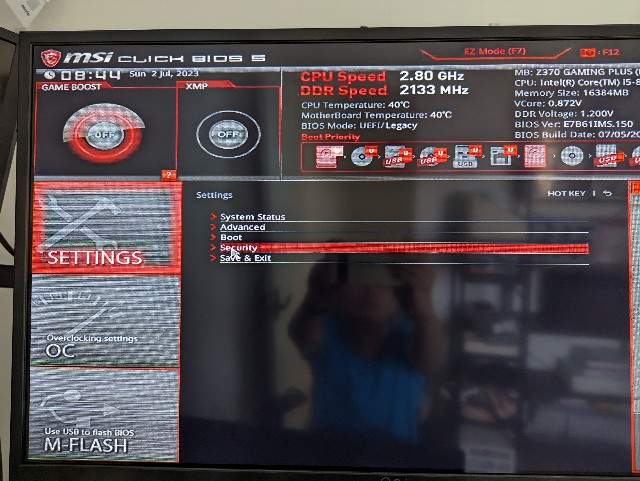
Advanced > Settings > Security > Trusted Computing をクリックします。

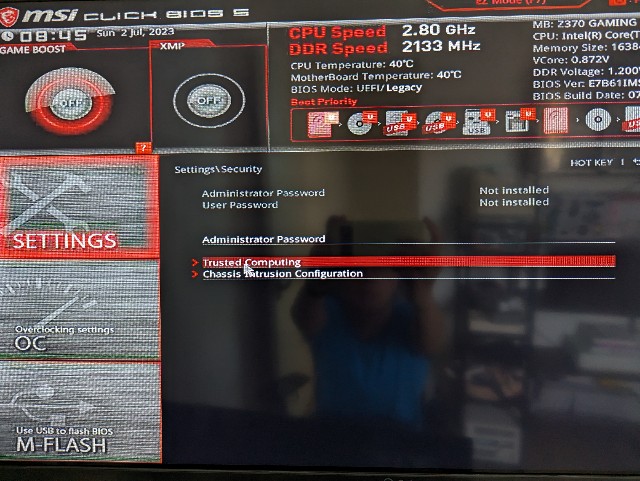
Advanced > Settings > Security > Trusted Computing > TPM Device Selection で "PTT" が選択されていることを確認します。
しかしながら上の項目 "Security Device Support" が Disabled の状態なので, "Enabled" に変更します。

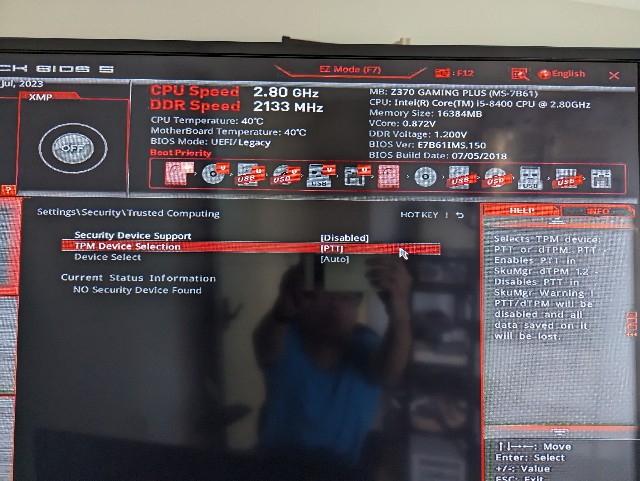
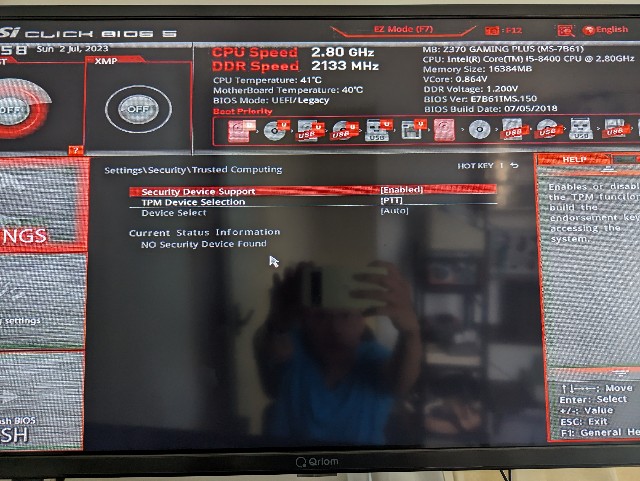
変更が完了したら, 変更を保存[F10]して, 再起動しましょう。

設定変更が反映された場合,
画面左下のタスクバーに"PC"と入力して「PC正常性チェック」アプリを起動 >「今すぐチェック」ボタンをクリックして
windows11対応可能性が確認できると思います。

Windows11へのUpdate作業は, 設定 > 更新とセキュリティ > Windows Update で行うのですが, 設定変更直後はwindows11更新可能と認識しないことがあるので, しばらく経ってから更新作業をしてあげましょう。

以上が "このPCは現在、Windows 11を実行するための最小システム要件を満たしていません" への対処法になりました。

参考リンク
PC 正常性チェック アプリの使用方法 - Microsoft サポート
PC で TPM 2.0 を有効にする - Microsoft サポート

Windowsでディスプレイ表示を回転させる方法

エンジニアの方々マルチディスプレイ大好きな人, 多いですよね。
特にプログラミングをする場合には, ディスプレイを縦向きにしてコードを書きたい人が多いように思います。

今回はマルチディスプレイ初心者でも可能なように, ディスプレイ表示の回転設定変更について, 画面遷移を記録してメモします。

まずは画面右下のタスクバーから「設定アプリ」を起動します。
設定アプリ中の「システム」をクリックします。

設定(Windows Setting)

設定 -> システム の「ディスプレイ」をクリックします。(システム開いたら最初からディスプレイ設定なので何もしないでOK)

次に変更したいディスプレイをクリックして選択します。
どのディスプレイが目的のものか分からない場合には, 「識別」ボタンをクリックしたら, ディスプレイ上に番号が表示されますので, ご参考までに。

設定 -> システム -> ディスプレイ

目的ディスプレイを選択出来たら, 下にスクロールしていって, 「画面の向き」をクリックします。

設定 -> システム -> ディスプレイ -> 画面の向き

画面の向きを好きなものに変更してください。
画面の向きを変更したら, 「変更を維持しますか？」という画面が出るので、「変更を維持」をクリックしてください。

設定 -> システム -> ディスプレイ -> 画面の向き -> 変更する -> 変更を維持

以上で画面表示の回転設定が完了です。

それでは色んな向きのマルチディスプレイに囲まれるスマートな開発を楽しんでください！

鶏肉焼きとネギ塩ソース

今日から不定期で情報系男子大学院生の料理レシピ動画をアップしていきます．

初めは字幕つけようかと思っていたけど，面倒なので喋ることにしました．

まぁメモ的な扱いなので編集の労力をかけたくないという感じですね．

一番下に動画を載せておきます．

レシピを箇条書きで書いておきましょう．

材料

鶏肉焼き
・鶏肉(今回は骨付き) 300g程度
・塩 小さじ2杯
・胡椒 適量

ネギ塩ソース
・ネギ 1/3本
・塩 小さじ1杯
・グルタミン酸ナトリウム 微量
・中華スープの素 微量
・ごま油 大さじ1杯くらい?
・胡椒 適量
・ニンニク 入れるならチューブ0.3 cmくらい

調理行程

鶏肉焼き
1. 鶏肉に塩胡椒をまぶす．10-15分程度放置して肉に味を馴染ませる．
2. フライパンで焼く．皮目から弱火で焼くと皮の油で焼ける．ただし，皮目に塩胡椒を振った場合には，焦げ付く可能性がある．
3. 両面に焼き目がついたら水を少量入れて蓋をして15分くらい蒸す．鶏肉はしっかり火を通さないとカンピロバクターなどの感染症になる場合があるので，蒸してしっかり中まで火を通します．
4. 蒸し終わったら蓋をとって，強火で皮目を焼きながら水分を飛ばしていきます．大体皮目がパリッとしてきたら完成．

ネギ塩ソース(鶏肉15分蒸してる間にやりましょう)
1. ネギを縦に切って，適当な大きさに切って整えます．
2. 塩，胡椒，グルタミン酸ナトリウム, 中華スープの素, ごま油，ニンニクを入れて混ぜると完成．

鶏肉焼きにネギ塩ソースをかけて完成．

鶏肉焼きネギ塩スープ(おまけ)
骨付き鶏肉の骨まわりの肉をとるのは大変なので，茹でて外しやすくして食べます．
1. 骨付き鶏肉の残りとネギ塩ソースの残りをフライパンに入れて水を入れる．
2. 塩を小さじ1杯入れて茹でる．完成．

www.youtube.com
www.youtube.com

包丁の砥ぎ方撮ったけど砥ぎ方間違ってた草

料理のレシピを動画で記録しようと思って，アームのついてるカメラホルダー買ったんですよ．

ほんで何か試そうと思って，とりあえず包丁の砥ぎ方でも撮るかーって撮って，字幕つけて書き出したとこまではOK．

最後に包丁の砥ぎ方ちゃんと調べておこうと思って調べてみたら，ワイの撮った動画が砥ぎ方ミスってたことに気づいて，，，

もうええわ，なんか撮ったしとりあえずアップしよ．
ってことでアップします．

包丁の砥ぎ方撮ったけど砥ぎ方間違ってた草
www.youtube.com

ちなみに正しい砥ぎ方は，包丁の刃先を僕の動画と逆向きでやります．
包丁の研ぎ方|貝印包丁サイト

僕は今まで動画の砥ぎ方でちゃんと切れ味上がってます．

でも今後は正しい砥ぎ方で砥ぎます．

ABC-051 C-Back and Forth: AtCoder

ネタができるまで，暇な時にこれまで解いてきたAtCoderの過去問を上げていくことにしました．

問題文
イルカは x 軸正方向を右、 y 軸正方向を上とする 2 次元座標平面にいます。 イルカは現在点(sx, sy) にいて、 1 秒あたり上下左右に距離 1 だけ進むことができます。 このとき、移動前と移動後の x 座標、 y 座標はともに整数でなければなりません。 イルカはここから sx < tx と sy < ty を満たす点 (tx, ty) に行き、その後点 (sx, sy) に戻り、また点 (tx, ty) に行き、その後点 (sx, sy) に戻ります。 このとき、イルカは点 (sx, sy) と点 (tx, ty) を除いて、途中で同じ座標を複数回通らないように移動しなければなりません。 このような条件を満たすイルカの最短経路を 1 つ求めてください。

制約
−1000 ≦ sx < tx ≦ 1000, −1000 ≦ sy < ty ≦ 1000, sx, sy, tx, ty は整数である。

方針
目的地までの1往復目は最短経路，2往復目は最短経路の外を迂回する経路とする．目的地までの最短経路は，まずは目的地のx座標まで移動して，その後目的地のy座標まで移動する．帰路は逆周りで帰ってくる．
2往復目を考えます．1往復目において，出発地点の1マス上と1マス右は既に通った経路となるので通れません．そのため，2往復目は必ず，1マス下と1マス左を，往路と復路で使う必要があります．このような経路を考えると，以下の図のような経路を考えることができます．

赤：出発地点，青：目的地，灰：1往復目の経路，緑：2往復目の経路

これをc++で書いたものが以下のようになります．

#include <iostream>
 
using namespace std;
 
 
int main(){
    int sx,sy,tx,ty;
    cin >> sx >> sy >> tx >> ty;
    int R,L,U,D;
    R = tx-sx;
    L = R;
    U = ty-sy;
    D = U;
    for (int i = 0; i < R; i++) cout << "R";
    for (int i = 0; i < U; i++) cout << "U";
    for (int i = 0; i < L; i++) cout << "L";
    for (int i = 0; i < D; i++) cout << "D";
    cout << "D";
    for (int i = 0; i < R+1; i++) cout << "R";
    for (int i = 0; i < U+1; i++) cout << "U";
    cout << "L";
    cout << "U";
    for (int i = 0; i < L+1; i++) cout << "L";
    for (int i = 0; i < D+1; i++) cout << "D";
    cout << "R";
 
    return 0;
}

画像のフーリエ変換3: 走査トンネル顕微鏡(STM)でグラファイト(HOPG)を撮像し，FFTで鮮明化する．

今回は，画像のフーリエ変換を応用して，走査トンネル顕微鏡(STM)でグラファイト(HOPG)を撮像し，FFTで鮮明化します．

具体的にはこのような作業をします．

(左)STMによるHOPG撮像結果 (右)FFTとマスキング処理によって鮮明化

左側の画像に赤線がありますが，すいません，元画像は紛失しました．

作業途中のスクリーンショットのみ見つかったので，これで勘弁してください．

走査トンネル顕微鏡(STM)とは？グラファイト(HOPG)とは？と思っている方へ．

STMは，簡単に言うと針で物の表面形状を見る顕微鏡です．
測定対象の近くに針を極限まで近づけると，測定対象物の表面原子の持つ電子がSTMの針に移動します(トンネル効果)．
STMの針は電子を受け取って，その電流によって測定対象物の表面形状を測定できます．
ちなみにSTMの受け取る電流は，原子1個分の距離でも変化が読み取れるので，ナノスケールの測定に使われています．

HOPGは，簡単に言うと炭素です．
簡単に言うと，炭素の中でも，並び方がすごく綺麗な炭素のことをHOPGと呼びます．

詳しくは以下で↓
走査型トンネル顕微鏡 - Wikipedia
高配向性熱分解グラファイト - Wikipedia

さて，これまでにやってきたことを振り返る人へのリンクを置いておきます．

画像のフーリエ変換1は，FFTで具体的な画像へローパス・ハイパスフィルタをかけてみました．
画像のフーリエ変換 - werry-chanの日記．料理とエンジニアリング

画像のフーリエ変換2は，単調な波を使ってFFTの特性を理解しました．
pythonで画像のフーリエ変換2 - werry-chanの日記．料理とエンジニアリング

それでは，HOPGのSTM画像をFFTして鮮明にしましょう．

今回は，Igorというソフトウェアで解析を行います．

まずはHOPGのSTM画像をFFTしましょう．

(左)HOPG_STM像 (右)HOPG_STM像のFFTパワースペクトル画像

このFFT画像は，以前に行ったFFT画像と異なる様子がいくつかありますね．

1．縦に長い．
2．A,B,Cとか四角とか青い線が書いてある．
3．スケールバーがついている．

まず1．について説明します．
以前までのFFT画像を思い返してください．
全てのFFT画像は，原点対称だったような気がしませんか？
実は，以前までのFFT画像は原点対称でした．
ということは，重複する情報は除いた方が合理的です．
このような理由から，Igorでは左半分が省かれた，縦長のFFT画像になっています．

次に2．についてです．
A,B,Cとか資格とか青い線は，僕がこの後の作業の説明のために付しました．

3．はIgorのFFT画像の仕様です．

さて，続きに入りましょう．

パワースペクトル画像に対して，A,B,Cと点を付しています．

このABCは，FFT画像の主成分・ピーク(値が大きい領域)になります．

青い線は，中心からの方向が分かるように付してあります．

これらのA,B,Cそれぞれの近傍成分のみを抽出し，逆フーリエ変換してみましょう．

(左)A近傍iFFT (中央)B近傍iFFT (右)C近傍iFFT

このように主成分によっていくつかの波が抽出されます．

これらのA,B,C3つ全ての近傍を抽出して逆フーリエ変換するとこのようになります．

A,B,C近傍をiFFT

何か粒子っぽい像が見えますね．

粒子っぽいですが，粒子ではないです．

あくまでSTMは対象物の電子を測定しているので，見えている像は電子です．

電子に注目して今回のHOPG像を考察しましょう．

グラファイトの構造

グラファイトは上のように二つの構造が有名な物ですが，今回はα構造だと考えます．

理由は，FFT像であげられる主成分ABCの相対角度が約60°であったという解析結果です．

βは複雑で，α構造のような単調な画像スペクトルは得られないと考えます．

さて，次に測定結果から原子間距離を推定しましょう．

今回取得した元画像は，縦：横 = 4nm : 4nmでした．

そして，FFT像の原点とABC間の距離は約0.12です(今回は象限入れ替えしてないので，原点周辺が高周波成分で辺縁部が低周波成分です)．

周波数に直すと主成分周波数は1/0.12 ~ 8.3です．

4nmの画像に対して，主成分の波はピーク(絶対値ピーク)が16.6個存在します．

逆フーリエ変換後の画像を見て，実際に横一列で16or17個くらいの白点が確認できると思います．

それでは白点間の距離を算出します．

4 nm/16.6 ~= 0.24 nm ~= 2.4 Å

この白点間の距離は，STMで測定されたトンネル電流(電子)の主成分であることに注意してください．

先ほどのα型のグラファイトの構造を見てみます．

青線と赤線の交点間を最短距離で結ぶと正三角形ができる．

青線で描かれたグラファイトは最上層で，赤線で描かれたグラファイト層はその下の層です．

赤と青の二つの層で原子の重なり合う位置に注目して，それぞれを最短距離で結ぶと正三角形が浮かび上がります．

STMで測定された像の主成分とは，この正三角形の頂点に由来する物なのです．

STMは，グラファイトの電子雲が上層と下層で重なり合う位置が，トンネル電流が大きく，その位置を主成分として検出しているということです．

さて，それではベンゼン状に結合したグラファイトの原子間距離1.42 Åは既知としましょう．

そうすると，検出された正三角形の一辺の長さは，理論上はとなります．

解析結果の2.4 Åとほぼ一致していますね．

このようにして，画像のフーリエ変換はSTMの解析などに応用されています．

様々な分野で応用されていますので，また時間があれば紹介しましょう．

pythonで画像のフーリエ変換2

よくわからないですが，以前にあげた画像のフーリエ変換のページがアクセス多いので，その続きを書きましょう．

以前のページ
werry-chan.hatenablog.com

以前のページでは，具体的な画像に対して二次元フーリエ変換(2DFFT)を行っていました．

さらに，2DFFTの後にハイパスorローパスフィルタをかけることで成分分析を行いました．

応用編↓画像のフーリエ変換でSTM像を鮮明化
画像のフーリエ変換3: 走査トンネル顕微鏡(STM)でグラファイト(HOPG)を撮像し，FFTで鮮明化する． - werry-chanの日記．料理とエンジニアリング

さて，今回は2DFFTについて更なる理解を深めるために，単純なsin波画像を2DFFTしてみましょう．

今回使う画像はこちらです．

波数1のsin波画像

横向きにsin波が輝度で表されていますね．

画像の縦方向に関しては変化がなく，横方向に波が生じています．

これを2DFFTし，象限を入れ替え，パワースペクトル画像にするとこのようになります．

周波数1のsin波fft画像

よーく見てもらうと真ん中あたりに線があります．

線は横方向に伸びていますね．

このように横方向の変化を持つ波画像を2DFFTすると，波の方向に応じた成分が表示されます．

詳しくは後に語るとして，その他の方向に関しても試してみましょう．

次は縦方向の波画像とその2DFFTパワースペクトル画像がこうなります．↓．

周波数1のsin波画像_縦とその2DFFTパワースペクトル画像

よーく見ると縦方向の線が見えます．

次に斜め方向の波画像(傾き30°)です．

画像の生成過程でアフィン変換という回転方法を使ったため，少し画像が劣化しましたが，まぁ良いでしょう．

斜め方向の波画像(傾き30°)と2DFFTパワースペクトル画像がこうなります．↓

周波数1のsin波画像_傾き30°とその2DFFTパワースペクトル画像

アフィン変換による劣化の影響は，2DFFTで顕著に現れましたが，斜め30°方向に線が見えるかと思います．

このように，2DFFTによって画像中に含まれる単調な波の成分の方向が分かります．

さて，次に波の周波数を変えてみると，どのように2DFFTの結果が変わるか確認しましょう．

周波数1, 10, 100の横波画像を見てみます．

周波数1,10,100のsin波画像

これらの2DFFTパワースペクト画像が以下のようになります．

波数1,50,100のsin波画像の2DFFTパワースペクトル画像

かなり細い線なので，違いが分かりにくいですね．

30°傾いた画像で見てみると，画像の劣化のおかげか少し見やすくなっていますので，そちらも見てみましょう．

周波数1,10,50,100のsin波画像_傾き30°

周波数1,10,50,100のsin波画像_傾き30°の2DFFTパワースペクトル画像

原点から傾き30°の線上にある輝度に注目しましょう．

まず基本として，象限入れ替えを行ったパワースペクトル画像は，原点周辺が低周波成分，辺縁部にかけて次第に高周波成分を示しています．
画像のフーリエ変換 - werry-chanの日記．料理とエンジニアリング
こちらでも図で説明がありますので参考に↑

ということは周波数1は，原点周辺が明るく，周波数が高くなるにつれて辺縁部が明るくなると予想できます．

しかながら，出力されたパワースペクトル画像からはこのような傾向は顕著ではありません．

その理由として，高調波(主成分の周波数の整数倍の波)の影響が存在します．

具体的に説明しましょう．

周波数50の画像をみてみましょう．

周波数50の波_傾き30°の2DFFTパワースペクトル画像と強調画像

最も中央に近い白マークが周波数50の斜め波成分になります．

次にその隣に存在する白マークは周波数100，さらにその隣が周波数150と，次第に輝度が減少しながら高調波が表れます．

周波数100の2DFFTパワースペクトル画像の場合は，主成分が十分に大きいため，高調波が見えません．

周波数10の2DFFTパワースペクトル画像の場合は，拡大して確認すると，周波数10とその高調波の成分(20,30,...)が確認できます．

周波数1の2DFFTパワースペクトル画像の場合は，主成分と高調波の間隔が狭すぎるため，見た目上は直線になっています．

同様のことが横方向・縦方向の波でも拡大することで確認できます．

しかしながら縦方向・横方向の波は，ノイズのない画像のため，2 px幅の線で表されています．

かなり拡大しないと確認は難しいでしょう．

以上のようにして，2DFFTパワースペクトル画像の各点の表す意味が理解できたかと思います．

・中央からの方向は，波の進行方向を表す．
・輝度は，波の強度(振幅)を表している．
・FFTは，高調波成分も検出する．

簡単に試せるソースコードを置いておきますね．

import cv2
import numpy as np


width,length = 800,800 #画像のサイズ
img = np.zeros((width,length),dtype = np.uint8) #画像の生成
wave_number = 100 #周波数
sin_row = np.sin(np.linspace(-wave_number*np.pi, wave_number*np.pi, 800)) #sin波の生成
sin_row = np.array(np.abs(sin_row*200), dtype = np.uint8) #輝度値に変換(max200とした)

#横波画像の生成
for i in range(len(img)):
    img[i] = sin_row

#img = np.transpose(img) #縦波に変換

#アフィン変換
degree = 30 #回転角度(°)
scale = 2 #拡大縮尺
trans = cv2.getRotationMatrix2D((int(width/2),int(length/2)), degree, scale)
img = cv2.warpAffine(img, trans, (width,length))
cv2.imwrite("sin.jpg",img)


#画像の二次元フーリエ変換
fimg=np.fft.fft2(img)
fimg = np.fft.fftshift(fimg)

#パワースペクトル化する
fimg= np.array(10*np.log(np.abs(fimg)+1),dtype = np.uint8)
print(np.where(fimg == np.max(fimg)))

cv2.imwrite("fft.jpg",fimg)